На практике часто приходится вычислять интегралы трансцендентных функций, которые содержат тригонометрические функции. В рамках этого материала мы опишем основные виды подынтегральных функций и покажем, какие методы можно использовать для их интегрирования.
Интегрирование синуса, косинуса, тангенса и котангенса
Начнем с методов интегрирования основных тригонометрических функций – sin , cos , t g , c t g . Используя таблицу первообразных, сразу запишем, что ∫ sin x d x = - cos x + C , а ∫ cos x d x = sin x + C .
Для вычисления неопределенных интегралов функций t g и c t g можно воспользоваться подведением под знак дифференциала:
∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C
Как же у нас получились формулы ∫ d x sin x = ln 1 - cos x sin x + C и ∫ d x cos x = ln 1 + sin x cos x + C , взятые из таблицы первообразных? Поясним только один случай, поскольку второй будет понятен по аналогии.
Используя метод подстановки, запишем:
∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2
Здесь нам нужно интегрировать иррациональную функцию. Берем тот же метод подстановки:
∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 · 1 - z 2 = ∫ d z z 2 - 1 = ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C
Теперь производим обратную замену z = 1 - t 2 и t = sin x:
∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C
Отдельно разберем случаи с интегралами, которые содержат степени тригонометрических функций, таких, как ∫ sin n x d x , ∫ cos n x d x , ∫ d x sin n x , ∫ d x cos n x .
О том, как их правильно вычислять, можно прочесть в статье об интегрировании с использованием рекуррентных формул. Если вы знаете, каким образом выведены эти формулы, то легко сможете брать интегралы вроде ∫ sin n x · cos m x d x с натуральными m и n .
Если у нас имеется комбинация тригонометрических функций с многочленами или показательными функциями, то их придется интегрировать по частям. Советуем прочесть статью, посвященную методам нахождения интегралов ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a · x · cos (a x) d x .
Наиболее сложными являются задачи, в которых подынтегральная функция включает в себя тригонометрические функции с разными аргументами. Для этого нужно пользоваться основными формулами тригонометрии, так что желательно помнить их наизусть или держать запись под рукой.
Пример 1
Найдите множество первообразных функции y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .
Решение
Воспользуемся формулами понижения степени и запишем, что cos 2 x 2 = 1 + cos x 2 , а cos 2 2 x = 1 + cos 4 x 2 . Значит,
y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) = sin (4 x) + 2 · 1 + cos 4 x 2 sin x · cos (3 x) + 2 · 1 + cos x 2 - 1 · sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x)
В знаменателе у нас стоит формула синуса суммы. Тогда можно записать так:
y = sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x) = = 1 + cos (4 x) sin (4 x)
У нас получилась сумма 3-х интегралов.
∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 · ln cos 4 x - 1 + C
В некоторых случаях тригонометрические функции, находящиеся под интегралом, можно свести к дробно рациональным выражениям с использованием метода стандартной подстановки. Для начала возьмем формулы, которые выражают sin , cos и t g через тангенс половинного аргумента:
sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2
Также нам нужно будет выразить дифференциал d x через тангенс половинного угла:
Поскольку d t g x 2 = t g x 2 " d x = d x 2 cos 2 x 2 , то
d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2
Таким образом, sin x = 2 z 1 + z 2 , cos x 1 - z 2 1 + z 2 , t g x 2 z 1 - z 2 , d x = 2 d z 1 + z 2 при z = t g x 2 .
Пример 2
Найдите неопределенный интеграл ∫ d x 2 sin x + cos x + 2 .
Решение
Используем метод стандартной тригонометрической подстановки.
2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3
Получим, что ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .
Теперь мы можем разложить подынтегральную функцию на простейшие дроби и получить сумму двух интегралов:
∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C
∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C
Ответ: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C
Важно отметить, что те формулы, которые выражают фукнции через тангенс половинного аргумента, не являются тождествами, следовательно, получившееся в итоге выражение ln t g x 2 + 1 t g x 2 + 3 + C – это множество первообразных функции y = 1 2 sin x + cos x + 2 только на области определения.
Для решения других типов задач можно использовать основные методы интегрирования.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Таблица первообразных ("интегралов"). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
|
Таблица первообразных ("интегралов"). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). |
|
|
Интеграл степенной функции. |
Интеграл степенной функции. |
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
|
Интеграл экспоненты, где a-постоянное число. |
|
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
Интеграл, равняющийся натуральному логорифму. |
Интеграл: "Длинный логарифм". |
|
Интеграл: "Длинный логарифм". |
|
|
Интеграл: "Высокий логарифм". |
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму. |
|
Интеграл: "Высокий логарифм". |
|
|
Интеграл косинуса. |
Интеграл синуса. |
|
Интеграл, равный тангенсу. |
Интеграл, равный котангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу |
|
|
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
Интеграл равный косекансу. |
Интеграл, равный секансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
|
|
|
|
Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
Формулы интегрирования по частям. Правила интегрирования.
|
Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. |
|
|
Интегрирование произведения (функции) на постоянную: |
|
|
Интегрирование суммы функций: |
|
|
неопределенные интегралы: |
|
|
Формула интегрирования по частям определенные интегралы: |
|
|
Формула Ньютона-Лейбница определенные интегралы: |
Где F(a),F(b)-значения первообразных в точках b и a соответственно. |
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x - независимая переменная, то:
|
Таблица производных. Табличные производные."таблица производный"-да, к сожалению, именно так их и ищут в интернете |
|
|
Производная степенной функции |
|
|
|
Производная экспоненты |
|
|
Производная экспоненциальной функции |
|
Производная логарифмической функции |
|
|
Производная натурального логарифма функции |
|
|
|
|
|
Производная косеканса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная арккотангенса |
|
|
|
|
|
Производная арккосеканса |
|
|
|
|
|
|
|
|
|
Производная
сложной экспоненциальной функции
Производная
натурального логарифма
Производная
синуса
Производная
косинуса
Производная
секанса
Производная
арксинуса
Производная
арккосинуса
Производная
арксинуса
Производная
арккосинуса
Производная
тангенса
Производная
котангенса
Производная
арктангенса
Производная
арккотангенса
Производная
арктангенса
Производная
арксеканса
Производная
арккосеканса
Производная
арксеканса
Производная
гиперболического синуса
Производная
гиперболического синуса в английской
версии
Производная
гиперболического косинуса
Производная
гиперболического косинуса в английской
версии
Производная
гиперболического тангенса
Производная
гиперболического котангенса
Производная
гиперболического секанса
Производная
гиперболического косеканса|
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. |
|
|
Производная произведения (функции) на постоянную: |
|
|
Производная суммы (функций): |
|
|
Производная произведения (функций): |
|
|
Производная частного (функций): |
|
|
Производная сложной функции: |
|
Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
|
|
|
|
|
|
|
|
|
|
|
Основное логарифмическое тождество |
|
|
Покажем как можно любую функцию вида a b сделать экспоненциальной. Поскольку функция вида е х называется экспоненциальной, то |
|
|
Любая функция вида a b может быть представлена в виде степени десяти |
|
Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045…) ln(e)=1; ln(1)=0
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1)
,
где f(x) - функция, имеющая при х=а производные
всех порядков. R n
- остаточный член в ряде Тейлора
определяется выражением
2)
k-тый коэффициент (при х k) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при
a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации (приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis - линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена(=Макларена, Тейлора в окрестностях точки 0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
|
|
|
|
|
|
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму
Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида
Воспользовавшись известными тригонометрическими формулами
(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам
(5)
(6)
Пример 1. Найти
Решение. По формуле (2) при
Пример 2. Найти интеграл от тригонометрической функции
Решение. По формуле (3) при
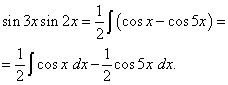
Пример 3. Найти интеграл от тригонометрической функции
Решение. По формуле (4) при
получаем следующее
преобразование подынтегрального выражения:
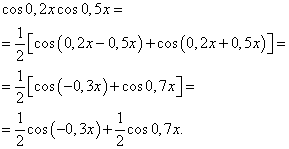
Применяя формулу (6), получим
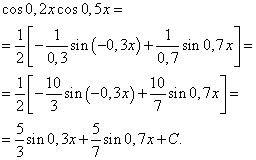
Интеграл произведения степеней синуса и косинуса одного и того же аргумента
Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.
(7)
В частных случаях один из показателей (m или n ) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sin x dx ) .
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что
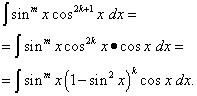
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t . Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx , выражая остальную часть подынтегральной функции через cos x и полагая t = cos x . Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса , когда хотя бы один из показателей - нечётный . Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения : когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится . Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.
Пример 4. Найти интеграл от тригонометрической функции
Решение. Показатель степени косинуса – нечётный. Поэтому представим
t = sin x (тогда dt = cos x dx ). Тогда получим
Возвращаясь к старой переменной, окончательно найдём
Пример 5. Найти интеграл от тригонометрической функции
.
Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим
и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим
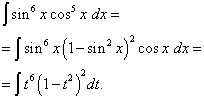
Раскроем скобки
и получим
Возвращаясь к старой переменной, получаем решение
Пример 6. Найти интеграл от тригонометрической функции
Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:
Тогда получим
Во втором интеграле произведём замену переменной, полагая t = sin2x . Тогда (1/2)dt = cos2x dx . Следовательно,
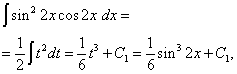
Окончательно получаем
Использование метода замены переменой
Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус - в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t , но и tgx = t и ctgx = t .
Пример 8. Найти интеграл от тригонометрической функции
.
Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:
.
Пример 9. Найти интеграл от тригонометрической функции
Решение. Преобразуем тангенс в отношение синуса и косинуса:
Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Пример 10. Найти интеграл от тригонометрической функции
Решение. Произведём замену переменной: , тогда .
Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество
:
Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt ). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Универсальная тригонометрическая подстановка
Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:
Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.
Пример 12. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой
. Тогда
.
Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда
Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).
СодержаниеСм. также:
Метод интегрирования по частям
Таблица неопределенных интегралов
Методы вычисления неопределенных интегралов
Основные элементарные функции и их свойства
Формула интегрирования по частям
При решении примеров этого раздела, используется формула интегрирования по частям:
;
.
Примеры интегралов, содержащих произведение многочлена и sin x, cos x или e x
Вот примеры таких интегралов:
, , .
Для интегрирования подобных интегралов, многочлен обозначают через u , а оставшуюся часть - через v dx . Далее применяют формулу интегрирования по частям.
Ниже дается подробное решение этих примеров.
Примеры решения интегралов
Пример с экспонентой, е в степени х
Определить интеграл:
.
Введем экспоненту под знак дифференциала:
e - x dx = - e - x d(-x) = - d(e - x)
.
Интегрируем по частям.
здесь
.
Оставшийся интеграл также интегрируем по частям.
.
.
.
Окончательно имеем:
.
Пример определения интеграла с синусом
Вычислить интеграл:
.
Введем синус под знак дифференциала:
Интегрируем по частям.
здесь u = x 2
,
v = cos(2
x+3)
,
du = (
x 2 )′
dx
Оставшийся интеграл также интегрируем по частям. Для этого вводим косинус под знак дифференциала.
здесь u = x
,
v = sin(2
x+3)
,
du = dx
Окончательно имеем:
Пример произведения многочлена и косинуса
Вычислить интеграл:
.
Введем косинус под знак дифференциала:
Интегрируем по частям.
здесь u = x 2 + 3
x + 5
,
v = sin 2
x
,
du = (
x 2 + 3
x + 5)′
dx